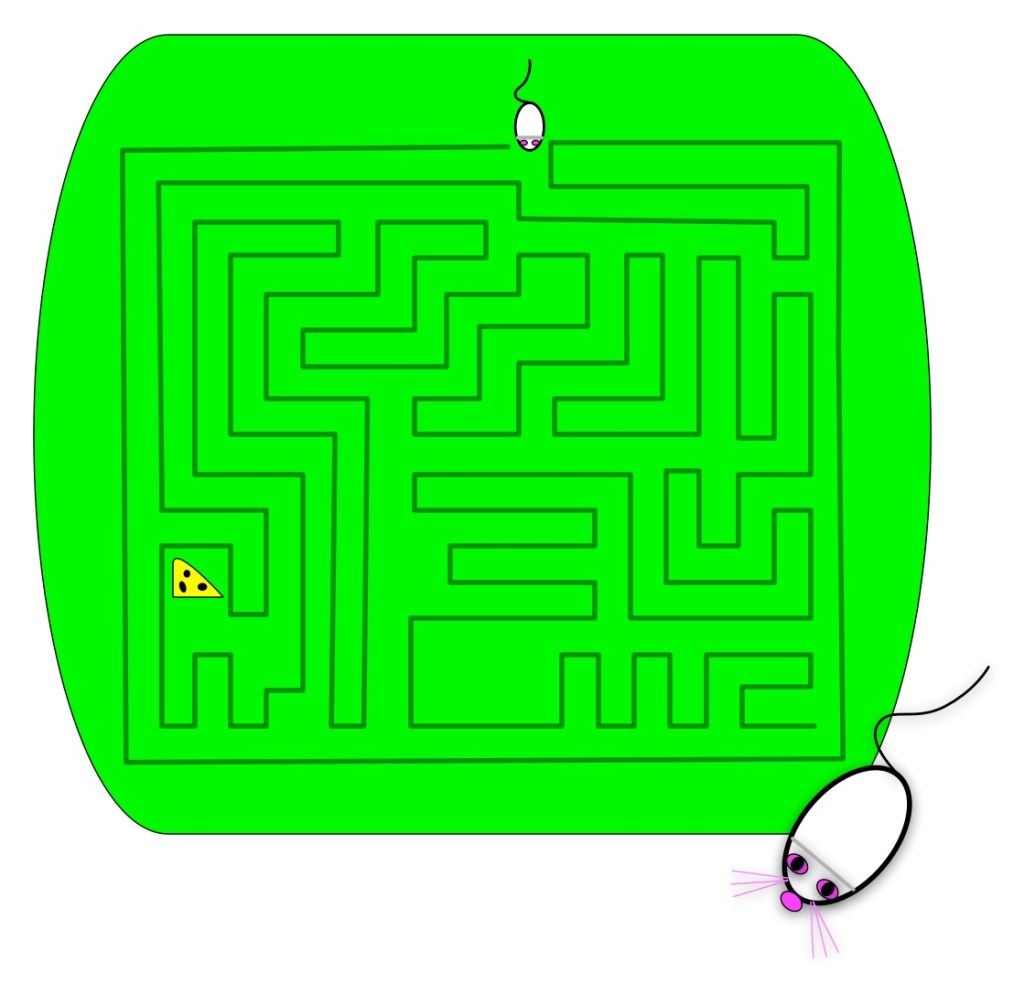
Solve the maze and show the mouse the way to the cheese.
Can you come up with an algorithm (a guaranteed way) for the mouse to find the cheese and escape from any maze?
Learn about what?
- What an algorithm is.
- How algorithms solve lots of similar problems.
- How those thinking up algorithms have to think of all the possibilities.
- There can be lots of totally different algorithms to solve the same problem.
More puzzles below…
Labyrinths, mazes and mindfulness
The words labyrinth and maze are often used interchangeably, but technically in English a labyrinth actually has just a single path with no junctions so no decisions to make at all. It is a ‘unicursal path’. This kind have been used as a form of mindfulness, or as a way to get closer to God. Mazes with choices so you could get lost in them, only really came to the fore when people started creating garden mazes with hedges as walls during the 16th century. One idea of the pure labyrinth is that walking it led to spiritual enlightenment. The more modern version of this is that walking one, with no choices to make, helps quieten the mind. This differs from the most famous use from Ancient Greek legend, where Daedalus built one to hold the half-man, half bull Minotaur monster.
Fun (and calming) to do
Make a pocket labyrinth out of clay. First make a circular clay tablet, then carve a labyrinth groove in it with a pencil. Bake it then keep it in your pocket and follow it with your finger if you ever feel anxious.
Spoiler alert: Maze algorithms …
Wall-following
To solve any maze of this kind, just follow one wall. So in a physical maze, put your hand (or whiskers) on the right hand wall and keep it there, as you walk round the maze. If you go in to dead ends this will automatically turn you round as you follow the wall round. Eventually you will get to the cheese, where ever it is and if you keep going you will eventually have walked round the whole maze and find yourself back at the exit. Try it.
With this algorithm branching mazes become no different to single path labyrinths (just imagine an invisible wall down the centre of the path you are following that stops short of dead ends!
Can this algorithm go wrong? Yes. It only works for certain kinds of mazes. For example, if the maze has multiple exits then you could come out of one of the other exits without having explored the whole maze. To allow for that, on leaving the maze from a different exit, treat the exit like a dead end and so carry on on the other side.
This illustrates an important property of algorithms. In creating algorithms you need to think of every possible situation and include instructions for any situation that can arise, as we just did for multiple exits. They must always work for the situation we claim them to be solutions for!
Are there any other potential problems that can arise? Our algorithm can also fail if the maze includes loops in them as then following a wall can take you round a circle back to where you started. It is an algorithm for solving mazes that are simply connected which means in this case all the walls/hedges are linked together. In terms of my drawing the maze in puzzle 1, I just drew the walls as a single, twisting and turning line. We have extended this to ones with multiple exits by imaging the exits have gates that connect the sides of the exit. A maze with a loop has spearate loops of hedges that are not linked to each other like opposite sides of a doughnut.
Can you think of a way to modify the algorithm so it still works even if there are loops? Can you think of other maze-solving algorithms?
Dead-end filling
Here is a completely different way to solve maze puzzles.
REPEAT the following until there are no dead-ends left:
- Find and mark with a cross a dead-end in the maze.
- Fill the maze in from the dead-end to the first junction you reach, removing the dead-end.
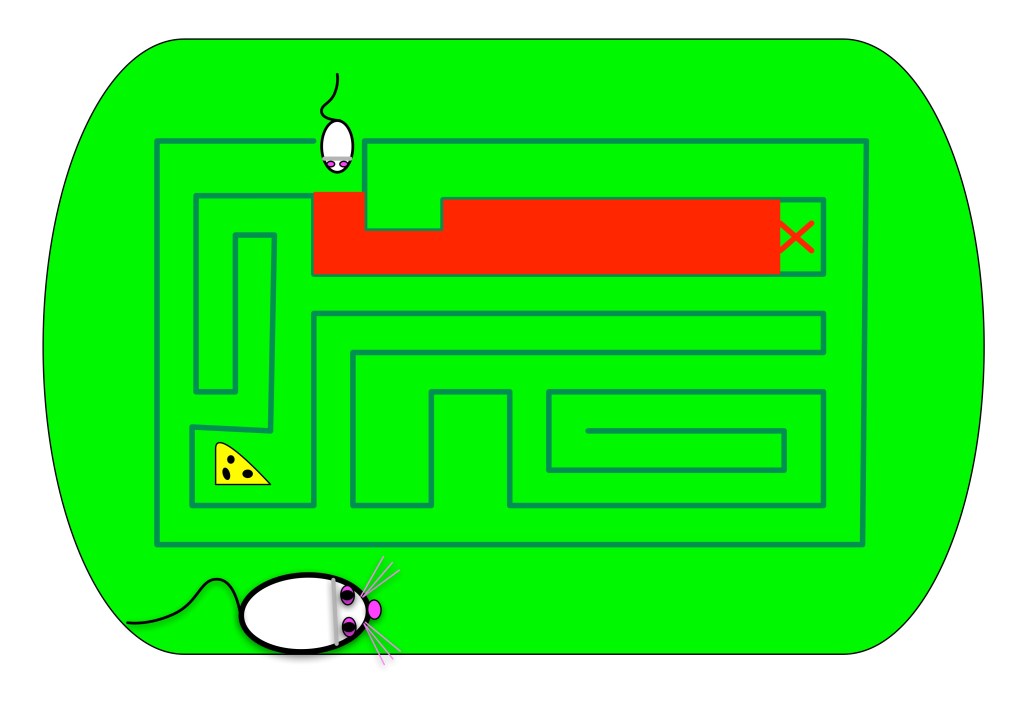
You are left with a labyrinth – a maze with a single path taking you straight to the cheese with no branches left to divert the mouse from the direct route.
This demonstrates how completely different algorithms can solve the same problem. The result of this algorithm though is a maze solution that is the most direct way to the centre of the maze, whereas wall-following potentially gives you a much slower route that explores a lot of the maze along the way.
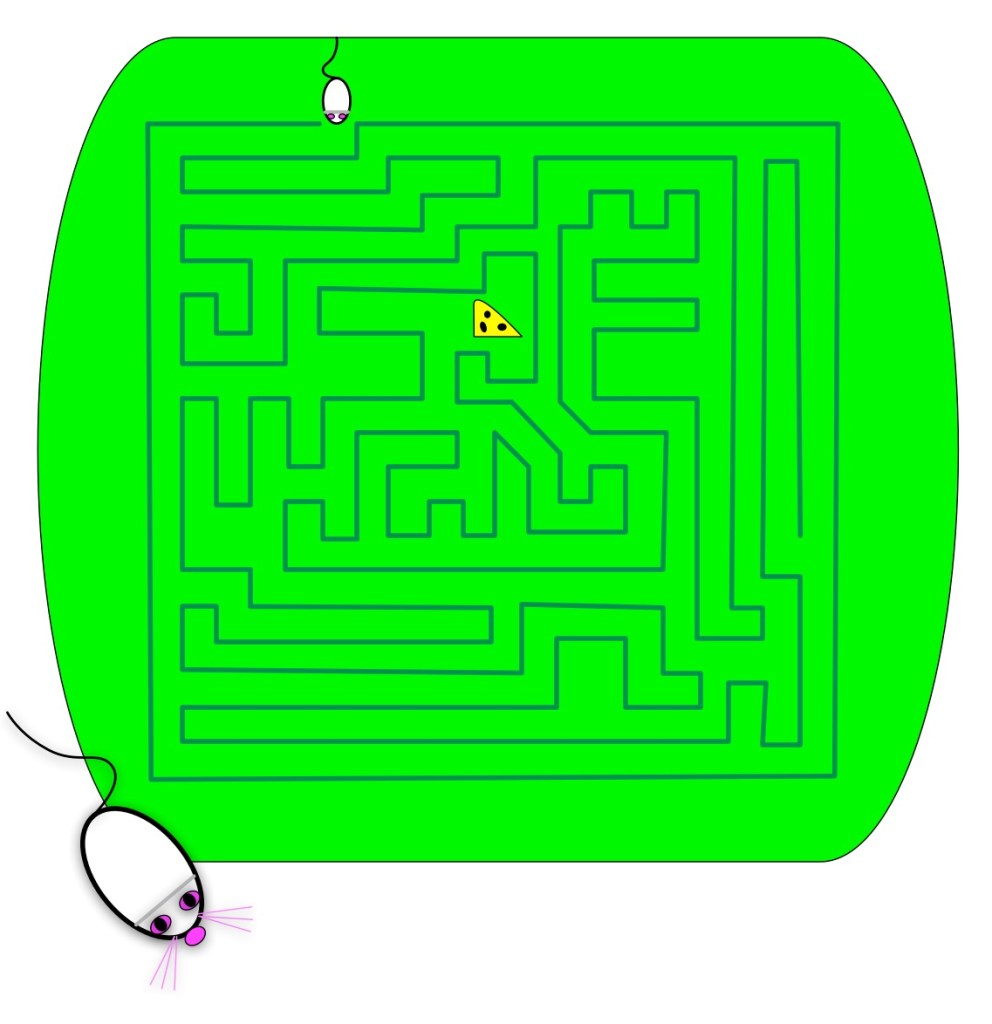
Puzzle 3
Solve this maze using the dead-end filling algorithm.
More Computer Science linked puzzles …
EPSRC supports Teaching London Computing and cs4fn through research grant EP/W033615/1.